...
...
domenica 31 gennaio 2010
venerdì 29 gennaio 2010
giovedì 28 gennaio 2010
martedì 26 gennaio 2010
sabato 23 gennaio 2010
giovedì 21 gennaio 2010
mercoledì 20 gennaio 2010
11x11eq121ids18
<<<
>>>
18 29 40 51 62 73 84 95
generano 40320 possibili permutazioni per configurazione
cmd x bdpq & free & ( E.S.E.)
>>>
18 29 40 51 62 73 84 95
generano 40320 possibili permutazioni per configurazione
cmd x bdpq & free & ( E.S.E.)
martedì 19 gennaio 2010
lunedì 18 gennaio 2010
venerdì 15 gennaio 2010
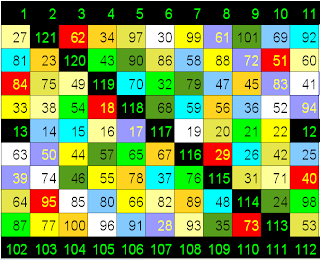
sono "sette", ricolorate simmetrie !
( ... una di quelle corrette è questa :)
...
abbinati colori nel "secondo quadro" blue|grigio_scuro e rosso|giallo_ocra
...
cmd x bdpq & free
...
abbinati colori nel "secondo quadro" blue|grigio_scuro e rosso|giallo_ocra
...
cmd x bdpq & free
simmetrie colorate per sette
( ... 4/49 ... ) rappresentati 4/7
... che coi colori diventa :
( notare 26 e 33 ... del primo quadro )
possibili sostituzioni ( un esempio ):
01 111317
02 113117
03 113717
04 117917
05 131317
06 133117
07 133717
08 137117
09 171317
10 171917
11 173917
12 177917
13 179317
14 179717
15 179917
16 191717
17 197117
18 313717
19 317717
20 319117
21 373717
22 377717
23 391117
24 391717
25 711317
26 713117
27 713917
28 717317
29 719717
30 731117
31 737717
32 739117
33 771917
34 773117
35 773317
36 777317
37 791117
38 791317
39 793717
40 797917
41 911917
42 917117
43 917317
44 939317
45 971917
46 979117
47 979717
48 991717
49 999917
cmd x bdpq & free
... che coi colori diventa :
( notare 26 e 33 ... del primo quadro )
possibili sostituzioni ( un esempio ):
01 111317
02 113117
03 113717
04 117917
05 131317
06 133117
07 133717
08 137117
09 171317
10 171917
11 173917
12 177917
13 179317
14 179717
15 179917
16 191717
17 197117
18 313717
19 317717
20 319117
21 373717
22 377717
23 391117
24 391717
25 711317
26 713117
27 713917
28 717317
29 719717
30 731117
31 737717
32 739117
33 771917
34 773117
35 773317
36 777317
37 791117
38 791317
39 793717
40 797917
41 911917
42 917117
43 917317
44 939317
45 971917
46 979117
47 979717
48 991717
49 999917
cmd x bdpq & free
giovedì 14 gennaio 2010
mercoledì 13 gennaio 2010
lunedì 11 gennaio 2010
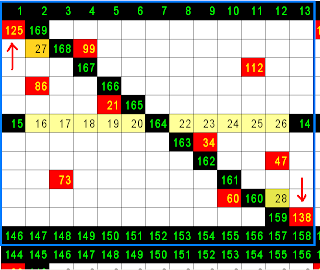
2/7 per derivare 1/25
1 di
608281864034267560872252163321295376887552831379210240000000000
possibili permutazioni ( 49 = 7 x 7 elementi ) :
[ vista parziale di 2 settimi ]
...
genera indicazione per 1 di
6138291366989258694349959882895972106599498609011003860555 \
4450350742292850928674636397530382746445436321611986015731 \
1612335467580920417813626276603324769117198699183678982737 \
8509013980470380923311175304252675031265068731159852575939 \
4065974095172206929419683558148645393895711305872054342823 \
6715159690516745444345158833048786544835756659847262787193 \
3600496167367365451591107357889563767378025674595258378197 \
7376815037742341507547496029909811742764200895316132012460 \
5838047740544264893127333986137362647557742010043063289809 \
5832127064795181051606377980897918161187501497859306309570 \
7930598941440055970814733678234847053536605100481169555823 \
9512255467210194894512284696400192559083685835956087607593 \
4622035248985308725542075856182586952561920126878472734768 \
9248312339067917854472083513026906895524560879388261740983 \
6259338427454009210704650731897687373289903157016420656748 \
7590007271780126381406228093914490964157014358524473819542 \
6974801440743661762091508076809659271580626204871046507401 \
7742747408893306713218992144860016361600335963025964761229 \
9810922197620699426516359663674118302369832218376455382891 \
0540019532891501570416088679438876747725038556590495084474 \
3461413084110462197771502692003511081520925746970398207599 \
9745882724592686046463010748963242110997715346128260903825 \
2193547534383573517418356160192763514392150016000000000000 \
0000000000000000000000000000000000000000000000000000000000 \
0000000000000000000000000000000000000000000000000000000000 \
0000000000000000000000000000
possibili permutazioni ( 625 = 25 x 25 elementi )
[ vista parziale di un venticinquesimo ]
cmd x bdpq & free & ( E.S.E. )
608281864034267560872252163321295376887552831379210240000000000
possibili permutazioni ( 49 = 7 x 7 elementi ) :
[ vista parziale di 2 settimi ]
...
genera indicazione per 1 di
6138291366989258694349959882895972106599498609011003860555 \
4450350742292850928674636397530382746445436321611986015731 \
1612335467580920417813626276603324769117198699183678982737 \
8509013980470380923311175304252675031265068731159852575939 \
4065974095172206929419683558148645393895711305872054342823 \
6715159690516745444345158833048786544835756659847262787193 \
3600496167367365451591107357889563767378025674595258378197 \
7376815037742341507547496029909811742764200895316132012460 \
5838047740544264893127333986137362647557742010043063289809 \
5832127064795181051606377980897918161187501497859306309570 \
7930598941440055970814733678234847053536605100481169555823 \
9512255467210194894512284696400192559083685835956087607593 \
4622035248985308725542075856182586952561920126878472734768 \
9248312339067917854472083513026906895524560879388261740983 \
6259338427454009210704650731897687373289903157016420656748 \
7590007271780126381406228093914490964157014358524473819542 \
6974801440743661762091508076809659271580626204871046507401 \
7742747408893306713218992144860016361600335963025964761229 \
9810922197620699426516359663674118302369832218376455382891 \
0540019532891501570416088679438876747725038556590495084474 \
3461413084110462197771502692003511081520925746970398207599 \
9745882724592686046463010748963242110997715346128260903825 \
2193547534383573517418356160192763514392150016000000000000 \
0000000000000000000000000000000000000000000000000000000000 \
0000000000000000000000000000000000000000000000000000000000 \
0000000000000000000000000000
possibili permutazioni ( 625 = 25 x 25 elementi )
[ vista parziale di un venticinquesimo ]
cmd x bdpq & free & ( E.S.E. )
sabato 9 gennaio 2010
venerdì 8 gennaio 2010
giovedì 7 gennaio 2010
Iscriviti a:
Post (Atom)
